My research accomplishments
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % Standard Commands %%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%mathbb
%greek
%GREEK
%cal
%tilde
%bar %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % Math Commands %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%compactified moduli space
% % % % %SYMPLECTIC GEOMETRY % % % % %
% % % % %Hat Delbar % % % % %
% % % % %COLORS % % % % %% % % % %GROMOV-WITTEN LANGUAGE % % % % %
% % % % %THOM LANGUAGE % % % % %
% % % % %POLYFOLD LANGUAGE % % % % %
In 1994, Kontsevich and Manin stated the Gromov–Witten axioms. At the time, it was not possible for them to give a complete proof; the field of Gromov–Witten theory was not yet mature, and it would take years for a mathematically rigorous definition of a Gromov–Witten invariant to develop. In 2017, polyfold theory, as developed by Hofer, Wysocki, and Zehnder, was successful in giving a well-defined Gromov–Witten invariant for general symplectic manifolds.
The focus of my mathematical career has been in giving a complete proof of the Gromov–Witten axioms using the tools and techniques of polyfold Gromov–Witten invariants. In 2019, I succeeded in this research project.
My research accomplishments to date are the following:
- Following the work of Thom, I solved the Steenrod problem for closed orientable orbifolds, proving that the rational homology groups of a closed orientable orbifold have a basis consisting of classes represented by closed embedded full suborbifolds whose normal bundles have fiberwise trivial isotropy action.
- I proved that the polyfold Gromov–Witten invariants, originally defined via integration of differential forms, may equivalently be defined as intersection numbers against a basis of representing suborbifolds.
- I provided a general framework for proving that polyfold invariants are natural, and in particular demonstrated that the polyfold Gromov–Witten invariants do not depend on auxiliary choices.
- I constructed the universal curve polyfold on which it is possible to define the \(k\)th-marked point forgetting map and to pullback abstract perturbations.
- I gave a complete proof of the Gromov–Witten axioms for the polyfold Gromov–Witten invariants.
- I showed that the classical pseudocycle Gromov–Witten invariants, defined for semipositive symplectic manifolds, are a strict subset of the more general polyfold Gromov–Witten invariants.
1 History of the Gromov–Witten axioms
In 1985 Gromov published the paper “Pseudo holomorphic curves in symplectic manifolds”, laying the foundations for the modern study of pseudo holomorphic curves (also know as \(J\)-holomorphic curves) in symplectic topology (Gromov 1985). In this paper, Gromov proved a compactness result for the moduli space of \(J\)-holomorphic curves in a fixed homology class. This paper contained antecedents to the modern notion of the Gromov–Witten invariants in the proofs of the nonsqueezing theorem and the uniqueness of symplectic structures on \(\mathbb{C}P^2\).
Around 1988, inspired by Floer’s study of gauge theory on three manifolds, Witten introduced the topological sigma model (Floer 1988; Witten 1988). The invariants of this model are the “\(k\)-point correlation functions”, another precursor to the modern notion of the Gromov–Witten invariants. Witten also observed some of the relationships between these invariants and possible degenerations of Riemann surfaces (Witten 1991). Further precursors to the notion of the Gromov–Witten invariants can also be seen in McDuff’s classification of symplectic ruled surfaces (McDuff 1991).
In 1993 Ruan gave a modern definition of the genus-zero Gromov–Witten invariants for semipositive symplectic manifolds (Ruan 1996, 1994). At the end of 1993, Ruan and Tian established the associativity of the quantum product for semipositive symplectic manifolds, giving a mathematical basis to the composition law of Witten’s topological sigma model (Ruan and Tian 1995).
In 1994 Kontsevich and Manin stated the Gromov–Witten axioms, given as a list of formal relations between the Gromov–Witten invariants (Kontsevich and Manin 1994). At the time it was not possible for Kontsevich and Manin to give a proof of the relations they listed; the definition of the Gromov–Witten invariant (complete with homology classes from a Deligne–Mumford space) would require in addition new ideas involving “stable maps” (Kontsevich 1995). Hence they used to term “axiom” with the presumed meaning “to take for assumption without proof”/ “to use as a premise for further reasoning”. And indeed, from these starting assumptions they were able to establish foundational results in enumerative geometry, answers to esoteric questions such as:
Kontsevich’s recursion formula. Let \(d\geq 1\). How many degree \(d\) rational curves in \(\mathbb{C}P^2\) pass through \(3d - 1\) points in general position?
Moreover, in this paper they outlined some of the formal consequences of the axioms by demonstrating how to combine the invariants into a Gromov–Witten potential, and interpret the axioms as differential equations which the potential satisfies.
To varying extents, this work has predated the construction of a well-defined Gromov–Witten invariant in symplectic geometry for \(J\)-holomorphic curves of arbitrary genus, and for all closed symplectic manifolds. Efforts to construct a well-defined Gromov–Witten invariant constitute an ever growing list of publications, including but not limited to the following: (Li and Tian 1998; Fukaya and Ono 1999; Fukaya et al. 2012; Siebert 1996; Cieliebak and Mohnke 2007; McDuff and Wehrheim 2012, 2018, 2017; Ionel and Parker 2013; Pardon 2016). A discussion of some of the difficulties inherent in these approaches can be found in (Fabert et al. 2016). Similarly, there have been several efforts to prove the Gromov–Witten axioms (Fukaya and Ono 1999; McDuff and Salamon 2012; Castellano 2016).
Over the past two decades, Hofer, Wysocki, and Zehnder have developed a new approach to resolving transversality issues that arise in the study of \(J\)-holomorphic curves in symplectic geometry called polyfold theory (Hofer, Wysocki, and Zehnder 2007, 2009a, 2009b, 2017a, 2010b, n.d., 2010a, 2017b). This approach has been successful in constructing a well-defined Gromov–Witten invariant for arbitrary genus and for general symplectic manifolds (Hofer, Wysocki, and Zehnder 2017a).
With a fully general Gromov–Witten invariant finally defined rigorously, my research has fixated on answering the following question:
Is it finally possible to prove the Gromov–Witten axioms by using polyfold theory?
2 What is a Gromov–Witten invariant?
Let \((M,\omega)\) be a closed symplectic manifold of dimension \(\dim M = 2n\), and let \(J\) be a \(\omega\)-compatible almost complex structure. For a fixed homology class \(A\in H_2(M,{\mathbb Z})\), and for fixed integers \(g\geq 0\), \(k\geq 0\), we consider the set of \(J\)-holomorphic curves:
\[ {\mathcal M}_{A,g,k}(J) := \left\{ \begin{array}{c} u: (\Sigma_g,j) \to M \\ \{z_1,\ldots,z_k\}\in \Sigma_g \end{array} \biggm| \begin{array}{c} \tfrac{1}{2} (du+J\circ du\circ j)=0 \\ u_*[\Sigma_g] = A \end{array} \right\} \biggm/ \begin{array}{l} u \sim u\circ \phi, \\ \phi\in \text{Aut} \end{array} \]
consisting of smooth maps \(u:(\Sigma_g,j)\to M\) which satisfy the Cauchy–Riemann equation modulo reparametrization; here \((\Sigma_g,j)\) is a genus \(g\) Riemann surface and \(\text{Aut}\) is the automorphism group of the Riemann surface \((\Sigma_g,j)\) which preserves the ordering of the marked points.
Gromov proved this set has a natural compactification in (Gromov 1985), which was later refined into the stable map compactification of Kontsevich in (Kontsevich 1995), and thus we may also consider its compactification, the Gromov–Witten moduli space:
\[ \bar{\mathcal{M}}_{A,g,k} (J) := {\mathcal M}_{A,g,k} (J) \sqcup \{\text{stable nodal $J$-holomorphic curves}\}. \]
We seek to use this space to construct invariants of the symplectic manifold \(M\). To this end, we define the evaluation map which evaluates a stable curve on each marked point:
\[ ev: \bar{\mathcal{M}}_{A,g,k} (J) \to M\times \cdots \times M. \]
On the top stratum of non-noded stable \(J\)-holomorphic curves it is given by
\[ ev\left([(u,z_1,\ldots,z_k)] \right): = (u(z_1),\ldots, u(z_k)). \]
With the fixed integers \(g \geq 0\), \(k \geq 3\) we also consider the associated Deligne–Mumford space, the natural compactification of the space of configurations of a complex structure and \(k\)-marked points on a genus \(g\) Riemann surface modulo biholomorphic equivalence:
\[ \bar{\mathcal{M}}_{g,k} := \text{cl} \left(\{ j, \{z_1,\ldots,z_k\}\in \Sigma_g \mid j \text{ complex structure on } \Sigma_g, z_i\neq z_j \text{ if } i \neq j\} / \text{Aut} \right). \]
When \(g = 0\) this space is a finite-dimensional manifold, and when \(g\neq 0\) this space is a finite-dimensional orbifold, in either case of dimension \(\text{dim}\) \(\bar{\mathcal{M}}_{g,k} = 6g - 6 + 2k\) We may define a projection map from the Gromov–Witten moduli space to the Deligne–Mumford space which forgets the curve which maps to \(M\) and which stabilizes the resulting unstable domain components:
\[ \pi: \bar{\mathcal{M}}_{A,g,k} (J) \to \bar{\mathcal{M}}_{g,k}. \]
On the top stratum of non-noded stable \(J\)-holomorphic curves it forgets the map \(u\) and is given by
\[ \pi\left([(u,j,z_1,\ldots,z_k)]\right) := [(j,z_1,\ldots,z_k)]. \]
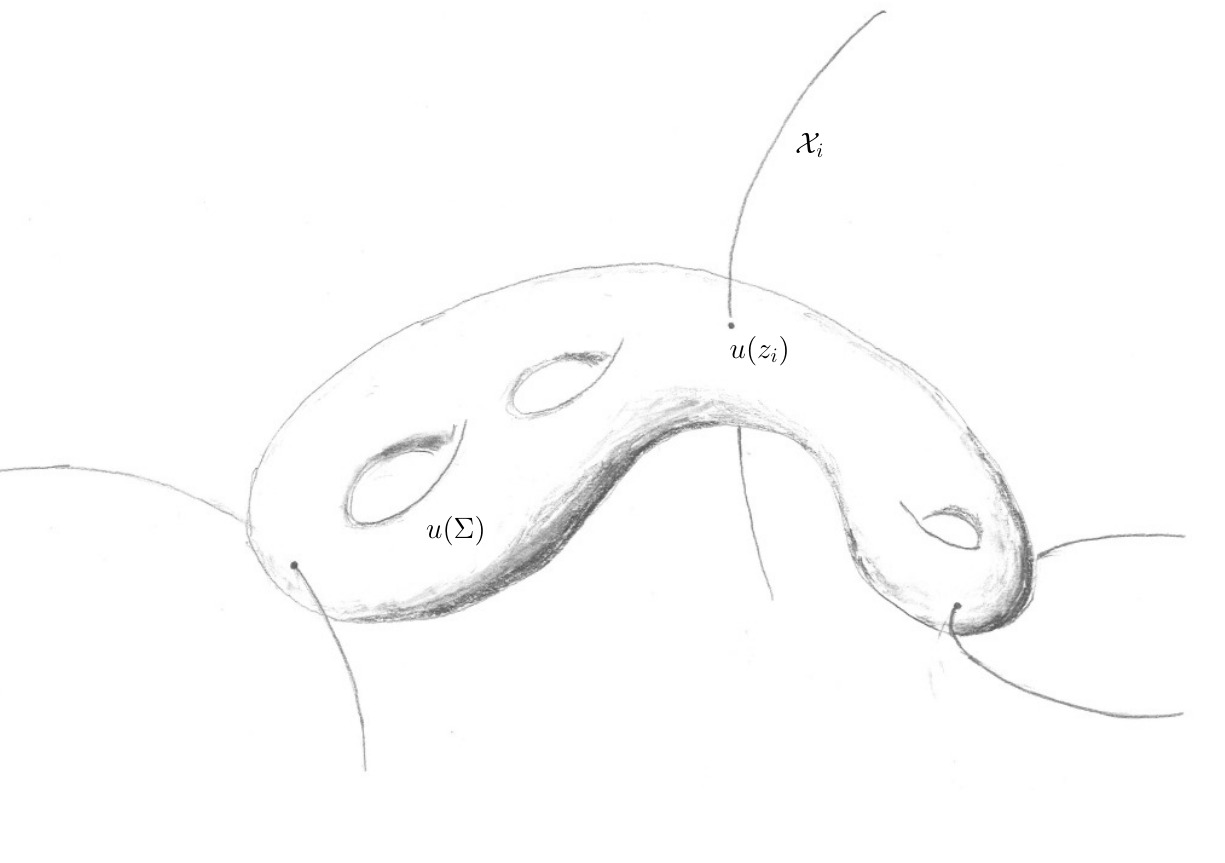
The traditional interpretation of a Gromov–Witten invariant is the (supposedly) finite count of \(J\)-holomorphic curves which at the \(i\)th-marked point pass through a submanifold \({\mathcal X}_i \subset M\) and whose marked point configuration is restricted by the projection map to a suborbifold \({\mathcal B}\subset \bar{\mathcal{M}}_{g,k}\). This can be visualized as the intersection number of the Gromov–Witten moduli space \(\bar{\mathcal{M}}_{A,g,k}(J)\) with the product suborbifold \({\mathcal X}_1\times \cdots \times {\mathcal X}_k \times {\mathcal B}\) via the map \(ev_1\times \cdots \times ev_k \times \pi\) as depicted in the following diagram:
\[ \begin{align*} \bar{\mathcal{M}}_{A,g,k}(J) \xrightarrow{ev_1\times \cdots \times ev_k \times \pi} M\times \cdots & \times M \times \bar{\mathcal{M}}_{g,k} \\ & \cup \\ {\mathcal X}_1\times \cdots &\times {\mathcal X}_k \times {\mathcal B}. \end{align*} \]
Such an intersection number should depend only on the homology classes of the submanifolds / suborbifolds, and should be independent of the almost complex structure. This count can be packaged algebraically as a homomorphism:
\[ \mathop{\mathrm{GW}}_{A,g,k} : H_*(M;{\mathbb Q})^{\otimes k} \times H_*(\bar{\mathcal{M}}_{g,k};{\mathbb Q}) \to {\mathbb Q}. \]
A foundational problem in symplectic geometry is to actually show that such a Gromov–Witten invariant is well-defined. Ideally, we would like to define a Gromov–Witten invariant rigorously via an intersection number:
\[ \mathop{\mathrm{GW}}_{A,g,k} ([{\mathcal X}_1],\ldots,[{\mathcal X}_k];[{\mathcal B}]) = (ev\times \pi) (\bar{\mathcal{M}}_{A,g,k} (J)) \cdot ({\mathcal X}_1\times \cdots \times {\mathcal X}_k \times {\mathcal B}), \]
or as an integral:
\[ \mathop{\mathrm{GW}}_{A,g,k} ([{\mathcal X}_1],\ldots,[{\mathcal X}_k];[{\mathcal B}]) = \int_{\bar{\mathcal{M}}_{A,g,k}(J)} ev^* (\mathop{\mathrm{PD}}[{\mathcal X}_1]\wedge \cdots \wedge \mathop{\mathrm{PD}}[{\mathcal X}_k]) \wedge \pi^* \mathop{\mathrm{PD}}[{\mathcal B}], \]
or as a pairing with a (virtual) fundamental class:
\[ \mathop{\mathrm{GW}}_{A,g,k} ([{\mathcal X}_1],\ldots,[{\mathcal X}_k];[{\mathcal B}]) = \left\langle (ev\times\pi)_* [\bar{\mathcal{M}}_{A,g,k}(J)], \mathop{\mathrm{PD}}[{\mathcal X}_1\times\cdots\times{\mathcal X}_k\times{\mathcal B}] \right\rangle. \]
Such definitions require additional structure on the Gromov–Witten moduli space; an intersection number requires tangent spaces and notions of transversal intersection, an integral requires smooth partitions of unity and notions of differential forms, and a (virtual) fundamental class requires a distinguished homology class on the topological space.
However, a priori, the Gromov–Witten moduli space only has the structure of a compact topological space, and this alone is insufficient to define any of the above. More structure is needed.
3 The classical pseudocycle Gromov–Witten invariant
The classical approach to defining the Gromov–Witten invariants is to show that the Gromov–Witten moduli space has the structure of a pseudocycle.
If the Cauchy–Riemann section were completely transversal to the zero section, i.e., transversal when considered on all possible nodal strata of the space of \(J\)-curves, then the top stratum of the space of \(J\)-curves would have the structure of a finite-dimensional manifold and all nodal strata would have the structure of manifolds with codimension at least \(2\) relative to the top stratum. Thus the space of \(J\)-curves would have the structure of a “pseudocycle”, i.e., a space whose boundary (the nodal strata) would be invisible from the point of view of homology.
Definition. Let \(M\) be a smooth manifold. A smooth map \(f: V \to M\) is a \(d\)-dimensional pseudocycle if \(V\) is an oriented \(d\)-dimensional manifold \(V\) such that the image \(f(V)\) has compact closure and such that the image of the boundary \(f(\bar{V} \setminus V)\) has dimension at most \(\leq d - 2\).
Pseudocycles have sufficient structure for defining intersection numbers, as for dimension reasons the boundary will not contribute to the intersection number.
However, transversality of the Cauchy–Riemann section is often impossible to obtain through classical techniques, i.e., perturbation of an almost complex structure. As a consequence, the nodal strata may have dimension larger than expected—indeed, larger than the dimension of the top stratum. This situation is a fundamental obstacle to the rigorous definition of a Gromov–Witten invariant; after all, for dimension reasons, any (nonzero) contribution to the intersection number from such a nodal stratum with large dimension would no longer be finite.
The pseudocycle approach to defining Gromov–Witten invariants deals with this difficulty by imposing strict conditions on the symplectic manifold which disallows such phenomena in the nodal strata. The “semipositive” condition was first introduced by McDuff in 1991 in (McDuff 1991): a symplectic manifold \((M^{2n},\omega)\) is called semipositive if, for every \(A\in \pi_2(M)\),
\[ \omega(A) >0,\ c_1(A) \geq 3-n \quad \implies \quad c_1(A) \geq 0. \]
This condition may seem ad-hoc, but it is specifically designed to guarantee that in the genus-zero case, the strata of nodal \(J\)-curves will have codimension at least \(2\) relative to the dimension of the top stratum of non-noded simple \(J\)-curves.
Theorem. (McDuff and Salamon 2012, Thms. 6.6.1, 6.7.1) Let \((M,\omega)\) be a semipositive sympletic manifold. There exists a regular almost complex structure on \(M\) such that the evaluation map from the genus-zero Gromov–Witten moduli space to the product \(M\times \cdots \times M,\)
\[ ev: \bar{\mathcal{M}}_{A,0,k}(J) \to M\times\cdots\times M, \]
is a pseudocycle.
The pseudocycle Gromov–Witten invariant is the homomorphism
\[ \text{pseudocycle-}\mathop{\mathrm{GW}}_{A,0,k} : H_* (M;{\mathbb Q})^{\otimes k} \to {\mathbb Q} \]
defined via the intersection number of the pseudocycle \(ev : {\mathcal M}^*_{A,0,k} (J) \to M\times\cdots\times M\) with a basis of representing submanifolds \({\mathcal X}\subset M\):
\[ \text{pseudocycle-}\mathop{\mathrm{GW}}_{A,0,k} ([{\mathcal X}_1],\ldots,[{\mathcal X}_k]) := ev({{\mathcal M}^*_{A,0,k}(J)}) \cdot \left({\mathcal X}_1 \times\cdots\times {\mathcal X}_k \right). \]
The invariant does not depend on the choice of regular almost complex structure \(J\), nor on the choice of representing basis.
4 The polyfold Gromov–Witten invariant
Polyfold theory, developed by Hofer, Wysocki, and Zehnder, is a modern approach to resolving transversality issues that arise in attempts to solve moduli space problems in symplectic geometry. The polyfold theoretic approach to solving a moduli space problem is to recast the problem into familiar terms from differential geometry. To do this, we may construct a “Gromov–Witten polyfold” \({\mathcal Z}_{A,g,k}\)—a massive, infinite-dimensional ambient space, designed to contain the entire unperturbed Gromov–Witten moduli space \(\bar{\mathcal{M}}_{A,g,k}(J)\) as a compact subset. We may furthermore construct a “strong polyfold bundle” \({\mathcal W}_{A,g,k}\) over \({\mathcal Z}_{A,g,k}\); the Cauchy–Riemann operator then defines a “scale smooth Fredholm section” of this bundle, \(\bar{\partial}_J:{\mathcal Z}_{A,g,k} \to {\mathcal W}_{A,g,k}\), such that \(\smash{\bar{\partial}_J}\vphantom{\partial}^{-1}(0) = \bar{\mathcal{M}}_{A,g,k}(J)\). We can construct “abstract perturbations” \(p\) of this section such that \(\bar{\partial}_J+p\) is transverse to the zero section and such that \((\bar{\partial}_J+p)^{-1}(0)\) is a compact set. In this way, we may take a scale smooth Fredholm section and “regularize” the unperturbed Gromov–Witten moduli space yielding a perturbed Gromov–Witten moduli space \({\mathcal S}_{A,g,k}(p):= (\bar{\partial}_J+p)^{-1}(0)\) which has the structure of a compact oriented “weighted branched orbifold”.
\[ \begin{array}{c} \bar{\mathcal{M}}_{A,g,k}(J) = \bar{\partial}_J^{-1}(0) \\ \text{\small{compact topological space}} \\ \end{array} \xrightarrow{\text{``polyfold regularization''}} \begin{array}{c} {\mathcal S}_{A,g,k}(p):=(\bar{\partial}_J+p)^{-1}(0) \\ \text{\small{compact ``weighted branched orbifold''}} \end{array} \]
This approach has been successful in giving a well-defined Gromov–Witten invariant for curves of arbitrary genus, and for all closed symplectic manifolds.
Consider homology classes \(\alpha_1,\ldots, \alpha_k \in H_* (M;{\mathbb Q})\) and \(\beta\in H_* (\smash{\bar{\mathcal{M}}}\vphantom{\mathcal{M}}^{\text{log}}_{g,k};{\mathbb Q})\). We can represent the Poincar'e duals of the \(\alpha_i\) and \(\beta\) by closed differential forms in the de Rahm cohomology groups, \(\mathop{\mathrm{PD}}(\alpha_i)\in H^*_{\mathop{\mathrm{dR}}} (M)\) and \(\mathop{\mathrm{PD}}(\beta)\in H^*_{\mathop{\mathrm{dR}}}(\smash{\bar{\mathcal{M}}}\vphantom{\mathcal{M}}^{\text{log}}_{g,k})\). By pulling back via the evaluation and projection maps, we obtain a closed \(\text{sc}\)-smooth differential form
\[ ev_1^* \mathop{\mathrm{PD}}(\alpha_1) \wedge \cdots \wedge ev_k^* \mathop{\mathrm{PD}}(\alpha_k) \wedge\pi^* \mathop{\mathrm{PD}}(\beta) \in H^*_{\mathop{\mathrm{dR}}} ({\mathcal Z}_{A,g,k}). \]
Theorem. (Hofer, Wysocki, and Zehnder 2017a, Thm. 1.12) The polyfold Gromov–Witten invariant is the homomorphism
\[ \mathop{\mathrm{GW}}_{A,g,k} : H_* (M;{\mathbb Q})^{\otimes k} \otimes H_* (\smash{\bar{\mathcal{M}}}\vphantom{\mathcal{M}}^{\text{log}}_{g,k}; {\mathbb Q}) \to {\mathbb Q} \]
defined via the “branched integration” of (Hofer, Wysocki, and Zehnder 2010a):
\[ \mathop{\mathrm{GW}}_{A,g,k} (\alpha_1,\ldots,\alpha_k;\beta) : = \int_{{\mathcal S}_{A,g,k}(p)} ev_1^* \mathop{\mathrm{PD}}(\alpha_1) \wedge \cdots \wedge ev_k^* \mathop{\mathrm{PD}}(\alpha_k) \wedge\pi^* \mathop{\mathrm{PD}}(\beta). \]
This invariant does not depend on the choice of perturbation.
5 Orbifolds and the Steenrod problem
The Steenrod problem was first presented in (Eilenberg 1949) and asked the following question:
Can any homology class of a finite polyhedron be represented as an image of the fundamental class of some manifold?
In (Thom 1954) Thom conclusively answered this problem, completely solving it for closed orientable manifolds.
Theorem (Thom 1954, Thm II.1) The rational homology groups of a closed orientable manifold have a basis consisting of classes represented by closed embedded submanifolds.
For solving this problem, and for his related work inventing cobordism theory, Thom was awarded the Fields medal in 1958. Aided by the modern language of ep-groupoids, I was able to follow the same approach as Thom and obtain the following analogue for orbifolds.
Theorem (Schmaltz 2019a, The Steenrod problem for orbifolds) The rational homology groups of a closed orientable orbifold have a basis consisting of classes represented by “closed embedded full suborbifolds whose normal bundles have fiberwise trivial isotropy action”.
In other words, given a closed orientable orbifold \(\mathcal{O}\) there exists a basis \(\{[\mathcal{X}_i]\}\) of the rational homology groups \(H_*(\mathcal{O};\mathbb{Q})\) which consists of the fundamental classes of such “closed embedded full suborbifolds \(\mathcal{X}_i\subset \mathcal{O}\) whose normal bundles have fiberwise trivial isotropy action”. Such a suborbifold is called a representing suborbifold.
Representing suborbifolds are well-suited for general intersection theories. Given such a suborbifold, the underlying topological space of the normal bundle is a vector bundle over the underlying topological space of the suborbifold. In contrast, the underlying topological space of an arbitrary orbifold bundle will generally not be a vector bundle. This means it is possible to use single valued sections (as opposed to multisections) for arguments involving perturbations.

6 Polyfold Gromov–Witten invariants as intersection numbers
The earliest interpretations of the Gromov–Witten invariants present in the literature were given in terms of counting a finite number of curves (McDuff and Salamon 2012; Ruan 1994, 1996). For example, Ruan described the Gromov–Witten invariants as a finite sum, counted with multiplicity, of nonmultiple cover \(J\)-spheres in \({\mathcal M}^*_{(A,J)}\) which intersect representatives of given cycles in the symplectic manifold (Ruan 1996, Thm. A).
However, such definitions have previously been restricted to genus zero Gromov–Witten invariants in semipositive symplectic manifolds. Observe that in the genus \(0\) case the Grothendieck–Knudsen spaces \(\smash{\bar{\mathcal{M}}}\vphantom{\mathcal{M}}^{\text{log}}_{0,k}\) are finite-dimensional manifolds. In contrast, if genus \(g >0\) the general Deligne–Mumford spaces \(\smash{\bar{\mathcal{M}}}\vphantom{\mathcal{M}}^{\text{log}}_{g,k}\) are orbifolds. Therefore, in the genus \(0\) case extant methods—such as representing a homology class as a pseudocycle in a manifold (zinger2008pseudocycles?) or, indeed, the Steenrod problem for manifolds—were sufficient to interpret the Gromov–Witten invariants as an intersection number.
Using the Steenrod problem for orbifolds, I was able to prove that the polyfold Gromov–Witten invariants may equivalently be defined as an intersection number. Let \({\mathcal S}_{A,g,k}(p)\) be a perturbed Gromov–Witten moduli space, and let \({\mathcal X}_1\times \cdots \times {\mathcal X}_k \times {\mathcal B}\) be a representing suborbifold of \(M^k \times \smash{\bar{\mathcal{M}}}\vphantom{\mathcal{M}}^{\text{log}}_{g,k}\).
I showed that transversality of a perturbed solution space of a polyfold with a representing submanifolds/suborbifolds may always be achieved through either of the following:
- Through the perturbation of the representing suborbifold; due to the properties of the normal bundle representing suborbifolds may always be perturbed (Schmaltz 2019a, Prop. 3.9).
- Assuming the map defined on the ambient polyfold is a submersion, we may obtain transversality through choice of a suitable abstract perturbation (Schmaltz 2019a, Prop. 3.10).
When \(\dim {\mathcal S}_{A,g,k}(p) + \dim \left({\mathcal X}_1 \times\cdots\times {\mathcal X}_k \times {\mathcal B}\right) = \dim (M^k \times \smash{\bar{\mathcal{M}}}\vphantom{\mathcal{M}}^{\text{log}}_{g,k})\) the intersection number is given by the signed weighted count of a finite number of points of intersection.
Theorem (Schmaltz 2019a, Polyfold Gromov–Witten invariants as intersection numbers) The polyfold Gromov–Witten invariant may equivalently be defined as the intersection number evaluated on a basis of representing submanifolds \({\mathcal X}\subset M\) and representing suborbifolds \({\mathcal B}\subset {\mathcal O}\):
\[ \mathop{\mathrm{GW}}_{A,g,k} ([{\mathcal X}_1],\ldots,[{\mathcal X}_k];[{\mathcal B}]) := \left(ev_1\times\cdots\times ev_k\times\pi\right)|_{{\mathcal S}_{A,g,k}(p)} \cdot \left({\mathcal X}_1 \times\cdots\times {\mathcal X}_k \times {\mathcal B}\right). \]
The invariant does not depend on the choice of abstract perturbation, nor on the choice of representing basis.
Thus the traditional geometric interpretation of the Gromov–Witten invariants as a “count of curves” is made literal.
7 A polyfold proof of the Gromov–Witten axioms
In 2019, I succeeded in giving a complete proof of the Gromov–Witten axioms.
Theorem (Schmaltz 2019c, Polyfold Gromov–Witten axioms) The polyfold Gromov–Witten invariants satisfy the Gromov–Witten axioms:
Effective axiom. If \(\omega(A)<0\) then \(\mathop{\mathrm{GW}}_{A,g,k} = 0\).
Grading axiom. If \(\mathop{\mathrm{GW}}_{A,g,k} (\alpha_1,\ldots,\alpha_k; \beta) \neq 0\) then
\[ \sum_{i=1}^k (2n - \deg (\alpha_i)) + (6g-6+2k - \deg(\beta)) = 2c_1(A) + (2n - 6)(1-g) + 2k. \]
Homology axiom. There exists a homology class
\[ \sigma_{A,g,k} \in H_{2c_1(A) + (2n-6)(1-g) + 2k} (M^k\times \bar{\mathcal{M}}_{g,k};{\mathbb Q}) \]
such that
\[ \mathop{\mathrm{GW}}_{A,g,k} (\alpha_1,\ldots,\alpha_k; \beta) = \langle p_1^* \mathop{\mathrm{PD}}(\alpha_1) \smallsmile \cdots \smallsmile p_k^*\mathop{\mathrm{PD}}(\alpha_k) \smallsmile p_0^*\mathop{\mathrm{PD}}(\beta), \sigma_{A,g,k} \rangle \]
where \(p_i: M^k \times \bar{\mathcal{M}}_{g,k} \to M\) denotes the projection onto the \(i\)th factor and the map \(p_0:M^k \times \bar{\mathcal{M}}_{g,k}\to\bar{\mathcal{M}}_{g,k}\) denotes the projection onto the last factor.
Zero axiom. If \(A=0,\ g=0\) then \(\mathop{\mathrm{GW}}_{0,0,k} (\alpha_1,\ldots,\alpha_k;\beta) = 0\) whenever \(\deg (\beta) >0\), and
\[ \mathop{\mathrm{GW}}_{0,0,k} (\alpha_1,\ldots,\alpha_k; [\operatorname{pt}]) = \int_M \mathop{\mathrm{PD}}(\alpha_1) \wedge \cdots \wedge \mathop{\mathrm{PD}}(\alpha_k). \]
Symmetry axiom. Fix a permutation \(\sigma: \{1,\ldots, k\}\to \{1,\ldots,k\}\). Consider the permutation map \(\sigma:\smash{\bar{\mathcal{M}}}\vphantom{\mathcal{M}}^{\text{log}}_{g,k}\to \smash{\bar{\mathcal{M}}}\vphantom{\mathcal{M}}^{\text{log}}_{g,k}, \ [\Sigma,j,M,D] \mapsto [\Sigma,j,M^\sigma,D]\) where \(M = \{z_1,\ldots,z_k\}\) and where \(M^\sigma := \{z'_1,\ldots,z'_k\},\) \(z'_i:= z_{\sigma(i)}\). Then
\[ \mathop{\mathrm{GW}}_{A,g,k} (\alpha_{\sigma(1)},\ldots,\alpha_{\sigma(k)}; \sigma_*\beta) = (-1)^{N(\sigma;\alpha_i)} \mathop{\mathrm{GW}}_{A,g,k} (\alpha_1,\ldots,\alpha_k; \beta) \]
where \(N(\sigma;\alpha_i):= \sharp \{ i<j \mid \sigma(i)> \sigma(j), \deg (\alpha_i)\deg(\alpha_j)\in 2{\mathbb Z}+1\}\).
Definition. (Kontsevich and Manin 1994, Eq. 2.3) We say that \((A,g,k)\) is a basic class if it is equal to one of the following: \((A,0,3)\), \((A,1,1)\), or \((A,g\geq 2,0)\).
The point is, for such values of \(g\) and \(k\) we will have \(\bar{\mathcal{M}}_{g,k-1} = \emptyset\) by definition.
Fundamental class axiom. Consider the fundamental classes \([M]\in H_{2n}(M;{\mathbb Q})\) and \([\smash{\bar{\mathcal{M}}}\vphantom{\mathcal{M}}^{\text{log}}_{g,k}] \in H_{6g-6+2k}(\smash{\bar{\mathcal{M}}}\vphantom{\mathcal{M}}^{\text{log}}_{g,k};{\mathbb Q})\). Suppose that \(A\neq 0\) and that \((A,g,k)\) is not basic. Then
\[ \mathop{\mathrm{GW}}_{A,g,k} (\alpha_1,\ldots,\alpha_{k-1},[M]; [\smash{\bar{\mathcal{M}}}\vphantom{\mathcal{M}}^{\text{log}}_{g,k}]) = 0. \]
Consider the canonical section \(s_i :\smash{\bar{\mathcal{M}}}\vphantom{\mathcal{M}}^{\text{log}}_{g,k-1} \to \smash{\bar{\mathcal{M}}}\vphantom{\mathcal{M}}^{\text{log}}_{g,k}\) defined by doubling the \(i\)th-marked point. Then
\[ \mathop{\mathrm{GW}}_{A,g,k} (\alpha_1,\ldots,\alpha_{k-1},[M]; s_{i*}\beta) = \mathop{\mathrm{GW}}_{A,g,k-1} (\alpha_1,\ldots,\alpha_{k-1};\beta). \]
Divisor axiom. Suppose \((A,g,k)\) is not basic. If \(\deg (\alpha_k) = 2n-2\) then
\[ \mathop{\mathrm{GW}}_{A,g,k} (\alpha_1,\ldots,\alpha_k; \mathop{\mathrm{PD}}(ft_k^* \mathop{\mathrm{PD}}(\beta))) = (A\cdot \alpha_k ) \ \mathop{\mathrm{GW}}_{A,g,k-1} (\alpha_1,\ldots,\alpha_{k-1};\beta), \]
where \(A\cdot \alpha_k\) is given by the homological intersection product.
Let \(\{e_\nu \} \in H^*(M;{\mathbb Q})\) be a homogeneous basis and let \(\{e^\mu \} \in H^*(M;{\mathbb Q})\) be the dual basis with respect to Poincaré duality, i.e., \(\langle e_\nu \smallsmile e^\mu, [M] \rangle = \delta_{\nu \mu}\). It follows from the Künneth formula that \(\{e_\nu \otimes e^\mu \}\) is a basis for \(H^*(M\times M;{\mathbb Q})\). We correct the sign by redefining \(e_\nu\) as \((-1)^{\deg e_\nu} e_\nu\). We can write the Poincaré dual of the diagonal \(\Delta \subset M\times M\) in this basis as \(\mathop{\mathrm{PD}}([\Delta]) = \sum_\nu e_\nu \otimes e^\nu\).
Splitting axiom. Fix a partition \(S_0 \sqcup S_1 =\{1,\ldots, k\}\). Let \(k_0 := \sharp S_0\), \(k_1 := \sharp S_1\) and let \(g_0\), \(g_1 \geq 0\) such that \(g = g_0 + g_1\), and \(k_i + g_i \geq 2\) for \(i=0,1\). Consider the natural map \[\phi_S : \bar{\mathcal{M}}_{k_0+1 , g_0}\times \bar{\mathcal{M}}_{k_1+1 , g_1} \to \bar{\mathcal{M}}_{g,k}\] which identifies the last marked point of a stable noded Riemann surface in \(\bar{\mathcal{M}}_{k_0+1 , g_0}\) with the first marked point of a stable noded Riemann surface in \(\bar{\mathcal{M}}_{k_1+1, g_1}\), and which maps the first \(k_0\) marked points of \(\bar{\mathcal{M}}_{g_0,k_0+1}\) to marked points indexed by \(S_0\) and likewise maps the last \(k_1\) marked points of \(\bar{\mathcal{M}}_{g_1,k_1+1}\) to marked points indexed by \(S_1\). Then
\[ \begin{align*} & \mathop{\mathrm{GW}}_{A,g,k} (\alpha_1, \ldots, \alpha_k; \phi_{S*} (\beta_0\otimes \beta_1) ) = (-1)^{N(S;\alpha)} \sum_{A_0+A_1 = A} \sum_\nu \\ & \qquad \mathop{\mathrm{GW}}_{A_0,g_0,k_0+1} (\{\alpha_i\}_{i\in S_0}, \mathop{\mathrm{PD}}(e_\nu) ; \beta_0) \cdot \mathop{\mathrm{GW}}_{A_1,g_1,k_1+1} (\mathop{\mathrm{PD}}(e^\nu), \{\alpha_j\}_{j\in S_1} ; \beta_1) \end{align*} \]
where \(N(S;\alpha)=\sharp \{j<i \mid i\in S_0, j\in S_1, \deg(\alpha_i)\deg(\alpha_j)\in 2{\mathbb Z}+1 \}\).
Genus reduction axiom. Consider the natural map \[\psi: \bar{\mathcal{M}}_{g-1,k+2} \to \bar{\mathcal{M}}_{g,k}\] which identifies the last two marked points of a stable noded Riemann surface, increasing the arithmetic genus by one. Then
\[ 2 \cdot \mathop{\mathrm{GW}}_{A,g,k} (\alpha_1, \ldots, \alpha_k; \psi_* \beta) = \sum_\nu \mathop{\mathrm{GW}}_{A,g-1,k+2} (\alpha_1,\ldots,\alpha_k, \mathop{\mathrm{PD}}(e_\nu) , \mathop{\mathrm{PD}}(e^\nu) ; \beta). \]
8 Strategy of the proof of the Gromov–Witten axioms
The Gromov–Witten axioms give relationships between the Gromov–Witten invariants. These relationships are determined by the geometry of certain naturally defined maps defined between the unperturbed Gromov–Witten moduli spaces, namely:
- permutation maps, \[\sigma : \bar{\mathcal{M}}_{A,g,k}(J) \to \bar{\mathcal{M}}_{A,g,k}(J),\]
- \(k\)th-marked point forgetting maps, \[ft_k : \bar{\mathcal{M}}_{A,g,k}(J) \to \bar{\mathcal{M}}_{A,g,k-1}(J),\]
- canonical sections, \[s_i : \bar{\mathcal{M}}_{A,g,k-1}(J) \hookrightarrow \bar{\mathcal{M}}_{A,g,k}(J).\]
Furthermore, using the map
\[ ev_{k_0+1} \times ev_1 : \bar{\mathcal{M}}_{A_0,g_0,k_0+1}(J) \times \bar{\mathcal{M}}_{A_1,g_1,k_1+1}(J) \to M\times M \]
we may consider the subset \((ev_{k_0+1} \times ev_1 )^{-1}(\Delta)\) of the product unperturbed Gromov–Witten moduli space with a constraint imposed by the diagonal \(\Delta \subset M\times M\). We then additionally have:
- inclusion maps, and maps \(\phi\) which identify the marked points \(z_{k_0+1}\) and \(z_1'\), \[ \begin{align*} \bar{\mathcal{M}}_{A_0,g_0,k_0+1}(J) & \times \bar{\mathcal{M}}_{A_1,g_1,k_1+1}(J) \\ i \bigg{\uparrow} & \\ (ev_{k_0+1} & \times ev_1 )^{-1}(\Delta) \xrightarrow{\phi} \bar{\mathcal{M}}_{A_0+A_1,g_0+g_1,k_0+k_1}(J) \end{align*} \] Likewise, using the map \(ev_{k+1} \times ev_{k+2} : \bar{\mathcal{M}}_{A,g-1,k+2}(J) \to M\times M\) we may consider the subset \((ev_{k+1} \times ev_{k+2} )^{-1}(\Delta)\) of the unperturbed Gromov–Witten moduli space with a constraint imposed by the diagonal \(\Delta \subset M\times M\). We then additionally have:
- inclusion maps, and maps \(\psi\) which identify the marked points \(z_{k+1}\) and \(z_{k+2}\) (increasing the arithmetic genus by one), \[ \begin{align*} \bar{\mathcal{M}}_{A,g-1,k+2}& (J) \\ i \bigg{\uparrow} \qquad &\\ (ev_{k+1} \times ev_{k+2}& )^{-1}(\Delta) \xrightarrow{\psi} \bar{\mathcal{M}}_{A,g,k}(J) \end{align*} \]
Intuitively, we should prove the Gromov–Witten axioms by interpreting the Gromov–Witten invariants as a finite count of curves and using the geometry of the above maps to directly compare such counts with respect to constraints imposed by the homology classes on \(M\) and \(\smash{\bar{\mathcal{M}}}\vphantom{\mathcal{M}}^{\text{log}}_{g,k}\).
A substantial amount of work is required to make this intuition rigorous in the context of an abstract perturbation theory. A deep understanding of the full machinery of polyfold theory, in addition to the geometry of the Gromov–Witten invariants is necessary to navigate substantial difficulties that we encounter.
9 Difficulties in proving the polyfold Gromov–Witten axioms
Proving this required a substantial amount of work, and relied on the results of (Schmaltz 2019b, 2019a). The Gromov–Witten axioms give relationships between the Gromov–Witten invariants. These relationships are determined by the geometry of certain naturally defined maps defined between the unperturbed Gromov–Witten moduli spaces, namely the permutation maps, the \(k\)th-marked point forgetting maps, in addition to certain natural maps which identify marked points into nodal pairs, where the Gromov–Witten moduli space is subject to a diagonal constraint. With the exception of the \(k\)th-marked point forgetting maps, we may pullback abstract perturbations in order to obtain well-defined restricted maps between perturbed Gromov–Witten moduli spaces.
The branched integral is useful for giving a well-defined definition of the polyfold Gromov–Witten invariants and moreover showing that they are, in fact, invariants and do not depend on choices. But integration is not the best viewpoint for giving a proof of all of the axioms. Intuitively, we should prove the Gromov–Witten axioms by interpreting the Gromov–Witten invariants as an intersection number and using the geometry of the above maps to directly compare such counts with respect to constraints imposed by the homology classes on \(M\) and \(\smash{\bar{\mathcal{M}}}\vphantom{\mathcal{M}}^{\text{log}}_{g,k}\). And indeed, via (Schmaltz 2019a) this intuition is made rigorous, and is precisely my approach to proving the axioms.
However, problems arise when we try to define a \(k\)th-marked point forgetting map between perturbed Gromov–Witten moduli spaces—such a map does not even exist. The construction of the smooth structure for the Deligne–Mumford orbifolds as described in (Hofer, Wysocki, and Zehnder 2017a) and (Hofer, Wysocki, and Zehnder, n.d.) requires a choice: that of a “gluing profile,” i.e., a smooth diffeomorphism \(\varphi: (0,1]\to [0,\infty).\) Given a noded Riemann surface and a nonzero parameter \(a \in {\mathbb C}\) we use the gluing profile to replace a region of the node with a cylinder of finite length \(\varphi(\lvert a\rvert)\). The logarithmic gluing profile is given by \(\varphi_{\log} (r) = -\frac{1}{2\pi} \log (r)\) and produces the classical holomorphic Deligne–Mumford orbifolds \(\smash{\bar{\mathcal{M}}}\vphantom{\mathcal{M}}^{\text{log}}_{g,k}\). There is also an exponential gluing profile, given by \(\varphi_{\exp} (r) = e^{1/r} - e\) which produces Deligne–Mumford orbifolds \(\smash{\bar{\mathcal{M}}}\vphantom{\mathcal{M}}^{\text{exp}}_{g,k}\) which are only smooth orbifolds. The exponential gluing profile is required for the scale smoothness of certain maps used to define the Gromov–Witten polyfolds.
This use of nonstandard smooth structure has the following consequence:
Problem 1. In general the map \(ft_k: \smash{\bar{\mathcal{M}}}\vphantom{\mathcal{M}}^{\text{exp}}_{g,k} \to \smash{\bar{\mathcal{M}}}\vphantom{\mathcal{M}}^{\text{exp}}_{g,k-1}\) is continuous but not differentiable.
Independent of the usage of a nonstandard gluing profile, there is no hope whatsoever of defining a \(k\)th-marked point forgetting map on the Gromov–Witten polyfolds as they are defined:
Problem 2. In general there does not exist a natural map \(ft_k\) on the Gromov–Witten polyfolds.
To explain, a stable curve in \({\mathcal Z}_{A,g,k}\) may contain a “destabilizing ghost component,” i.e., a component \(C_k\simeq S^2\) with precisely \(3\) special points, one of which is the \(k\)th-marked point, and such that \(\int_{C_k} u^*\omega=0,\) \(u|_{C_k} \neq\text{const}.\) After removal of the \(k\)th-marked point from such a component we cannot consider the resulting data as a stable curve in \({\mathcal Z}_{A,g,k-1}\).
We might try to restrict to a subset \({\mathcal Z}^\text{const}_{A,g,k}\subset {\mathcal Z}_{A,g,k}\) consisting of stable curves which are constant on such destabilizing ghost components. The \(k\)th-marked point forgetting map is then well-defined on this subset. However, if we consider \(\mathcal{Z}^\text{const}_{A,g,k}\subset \mathcal{Z}_{A,g,k}\) with the subspace topology, and \(\mathcal{Z}_{A,g,k-1}\) with the usual polyfold topology, then:
Problem 3. In general the well-defined restriction \(ft_k:{\mathcal Z}_{A,g,k}^\text{const} \to \mathcal{Z}_{A,g,k-1}\) is not continuous.
There is a final problem. In general, the projection map must factor through the \(k\)th-marked point forgetting map; this is due to the need to forget the added stabilizing points. Thus, in order to obtain a smooth projection map we must map to the logarithmic Deligne–Mumford orbifold. However:
Problem 4. While the projection \(\pi : {\mathcal Z}_{A,g,k} \to \smash{\bar{\mathcal{M}}}\vphantom{\mathcal{M}}^{\text{log}}_{g,k}\) is \(\text{sc}\)-smooth, in general it is not a submersion.
This has important consequences if we wish to consider the Gromov–Witten invariant as an intersection number; the only way to get transversality of the projection map with a representing suborbifold \({\mathcal B}\subset \smash{\bar{\mathcal{M}}}\vphantom{\mathcal{M}}^{\text{log}}_{g,k}\) is through perturbation of the suborbifold. This is made possible by the existence of representing suborbifolds, for which perturbation is possible, the existence of which is guaranteed by (Schmaltz 2019a).
10 The universal curve Gromov–Witten polyfold
In essence, the central problem is that the Gromov–Witten polyfolds as constructed are not “universal curves”. My proof of the Gromov–Witten axioms rectifies this by constructing a universal curve polyfold \({\mathcal Z}^\text{uc}_{A,g,k}\) over \({\mathcal Z}_{A,g,k-1}\), on which we may consider a well-defined \(k\)th-marked point forgetting map
\[ ft_k : {\mathcal Z}^\text{uc}_{A,g,k} \to {\mathcal Z}_{A,g,k-1}. \]
The preimage of stable curve in \({\mathcal Z}_{A,g,k-1}\) via \(ft_k\) can be identified with the underlying Riemann surface with nodes identified, thereby explaining the choice of nomenclature “universal curve”. It is possible to pullback regular perturbations via this map, and hence obtain a well-defined map between perturbed Gromov–Witten moduli spaces.
Now we find ourselves in the following situation: given the Gromov–Witten moduli space \(\bar{\mathcal{M}}_{A,g,k}\) we can define polyfold Gromov–Witten invariants associated to the usual Gromov–Witten polyfold \({\mathcal Z}_{A,g,k}\) and associated to the universal curve polyfold \({\mathcal Z}^\text{uc}_{A,g,k}\) which, a priori, we cannot assume are equivalent.
In (Schmaltz 2019b), I present a general framework for proving that polyfold invariants are natural, which applied to polyfold Gromov–Witten theory yields the following result.
Theorem. (Schmaltz 2019b, Naturality of the polyfold Gromov–Witten invariants) The polyfold Gromov–Witten invariants are natural, and do not depend on auxiliary choices made in their construction. In particular, the Gromov–Witten invariants associated to the usual Gromov–Witten polyfold and associated to the universal curve Gromov–Witten polyfold are identical.
11 Pseudocycle Gromov–Witten invariants are a strict subset of polyfold Gromov–Witten invariants
I unified the classical definition of a Gromov–Witten invariant as a pseudocycle and the modern definition of a Gromov–Witten invariant via polyfold theory by proving they are equivalent.
Theorem. (Schmaltz 2023, Main result) For a given semipositive symplectic manifold, the pseudocycle genus-zero Gromov–Witten invariants are equal to the polyfold genus-zero Gromov–Witten invariants.
Since the polyfold Gromov–Witten invariants are not restricted to genus-zero, nor to semipositive symplectic manifolds, we have
\[ \left\{ \begin{array}{c} \textit{pseudocycle} \\ \textit{Gromov-Witten} \\ \textit{invariants} \end{array} \right\} \subsetneq \left\{ \begin{array}{c} \textit{polyfold} \\ \textit{Gromov-Witten} \\ \textit{invariants} \end{array} \right\}. \]